これから，2問の問題が出題されます．それらの問題にはいくつかの式があり，そこには数ではなく，記号が書かれてあります．それらの記号には問題によって指定された数が当てはまり，同じ記号には同じ数，異なる記号には異なる数となります．その数は指定が無ければ整数とするとき，等式をすべて満たす記号の組合せを求めよ．(そのような組合せは私側のミスさえ無ければただ1つに定まります)
さあ，君は解くことが出来るだろうか．
第１問 2021年12月7日投稿 by エイジョン
【コメント】
１度修正をいれた問題です．それによって，解法が２つになってしまいました．解説は一方しか記載していないので，良かったら探してみては？
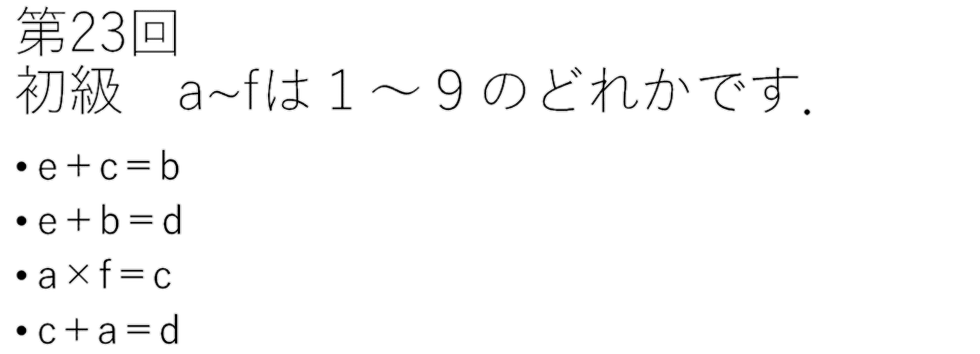
第２問 2021年12月7日投稿 by エイジョン
【コメント】
6，7つ目の式に当てはまる数の候補を考えます．
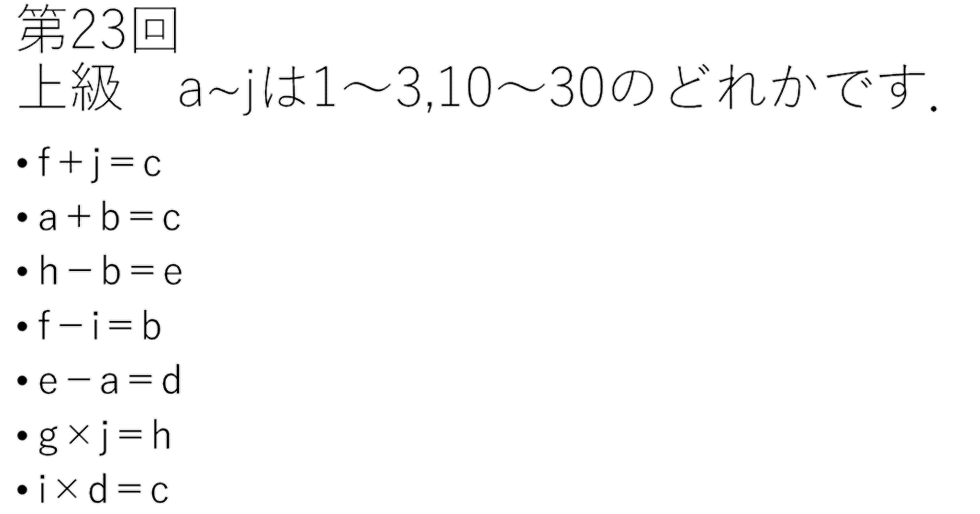
注：以下には解答解説があります．
現在１００問の問題作成まであと少しのところまで来ていて，もう１つ最難関を作りたいのですが（これで５問目），歴代最高で作成しづらい問題になってしまいました…
少しネタバレすると小数関係です．
次回の挑戦状は２０２２年１月４日投稿予定です．
〈解説に関する諸注意〉
説明不要かもしれませんが，解説にある～つ目の式という言葉がありますが，これはその解説に該当する問題の上から～番目の式を定義しています．2列ある場合は初めに左の列の式,次に右の列の式を定義するものとします．
